Diffusion Language Models Deep Dive (Part 1: Method)
Most language models today are autoregressive (AR): they generate tokens left-to-right, where the next token is decoded based on the previous ones.
In earlier posts I reviewed KV cache / memory considerations and scaling strategies for AR Transformers.
This post is my “future-me friendly” dive into Diffusion Language Models (DLMs), specifically the method: what the forward “noising” process is, what the reverse model predicts, and the objective formulation.
If you need a math review for the objectives defined below, they are also all provided in the previous post (Standard Diffusion Objective, KL, Variational Inference etc.)
I. Motivation
Q. Why even try diffusion for language when AR LMs work so well?
Diffusion offers a different generation regime:
- Iterative refinement instead of strict left-to-right decoding
- Potential for more parallelism during generation (update many positions at once)
The cost is that you trade a single left-to-right pass for multiple denoising steps.
II. The core question: what is “noise” in text?
Diffusion needs two pieces:
- a forward process that gradually corrupts clean data into “noise”
- a reverse process learned by a neural net that undoes the corruption
For images, the forward corruption is naturally Gaussian noise in pixel space.
For text, tokens are discrete, so we must decide what “corruption / noise” means.
This splits into two broad directions.
III. Continuous diffusion for text (historical stepping stone)
One early answer is: “make text continuous.”
- map tokens into a continuous space (embeddings or a latent),
- add Gaussian noise through time,
- learn a denoiser,
- decode denoised vectors back into discrete tokens.
A representative approach here is Diffusion-LM (2022, Percy Liang et al.), which performs diffusion in a continuous regime and then maps back to discrete text.
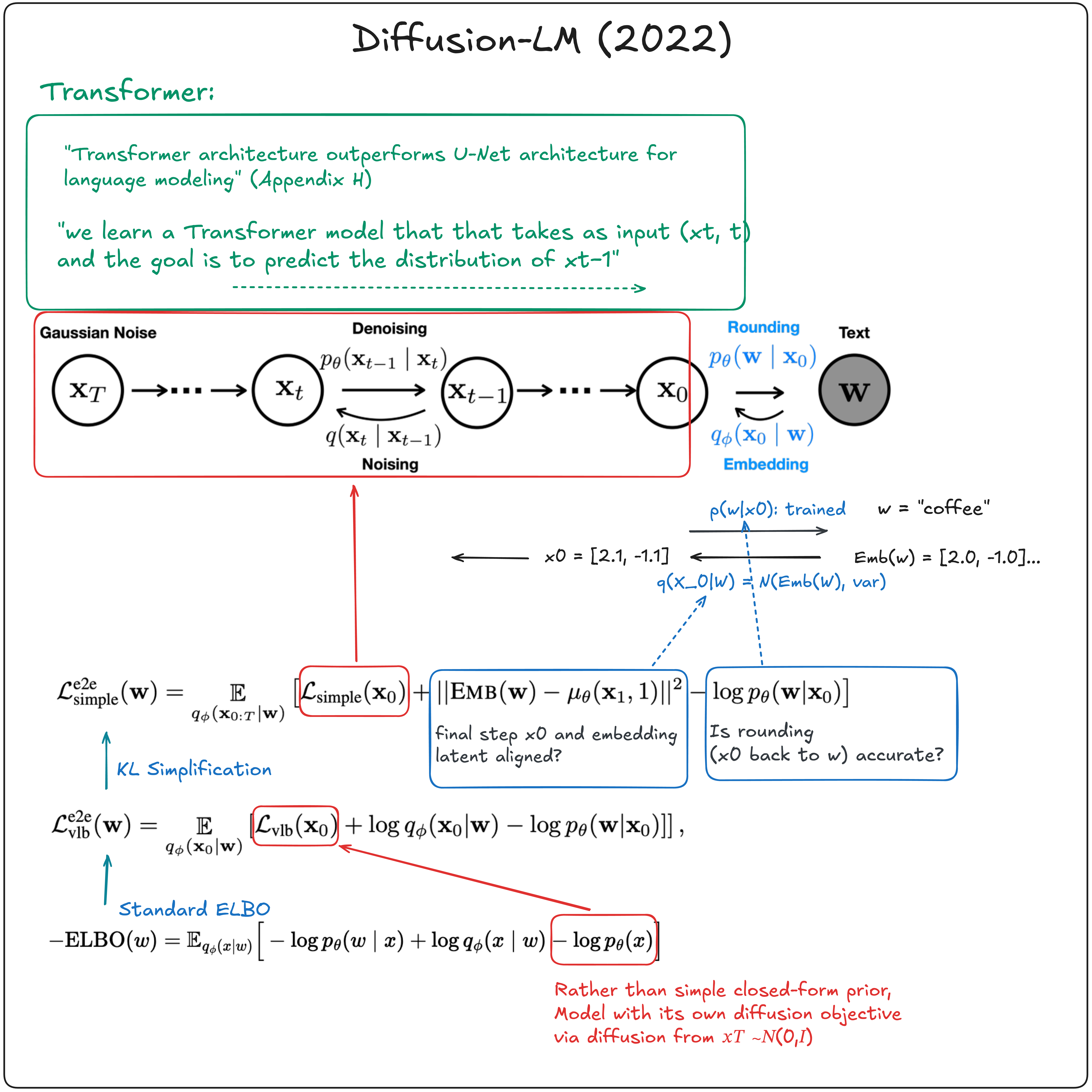
However, this continuous approach can struggle with fluency, because the final step requires rounding / mapping a denoised continuous vector back into a discrete token. If that rounding is even slightly off, small semantic errors can compound into noticeably less fluent text.
This motivates the more “native-to-language” view:
define diffusion directly on discrete token states, so we never need a continuous-to-discrete rounding step.
IV. Discrete diffusion
Text is discrete, so instead of adding Gaussian noise we can define a categorical corruption process over token states.
The key is: states are discrete, but transitions are probabilistic.
This figure is the full story: how the discrete Markov chain is defined, how the posterior drops out of Bayes’ rule, what normalization means, and why the “mask-as-absorbing-state” corruption is a natural fit for text.

Figure: Discrete diffusion posterior with a concrete matrix example.
The Core Takeaway before V.
Before diving into the next sections, some take-aways to keep in mind:
-
Forward Process is Categorical Unlike image diffusion that adds Gaussian blur, text diffusion operates on categorical transitions. We model noise as: \(q(x_t \mid x_0) = \mathrm{Cat}(x_t; x_0\bar Q_t)\) where $\bar Q_t = Q_1Q_2\cdots Q_t$ is the cumulative transition matrix.
-
Reparameterization: Predict $x_0$ Instead of learning tiny incremental steps ($x_t \to x_{t-1}$), we train the model to “peek” through the noise and predict the original $x_0$ from a noisy $x_t$. This $x_0$ prediction is then used to mathematically derive the reverse step.
-
[MASK]as an Absorbing State In text, noise is often “masking.” We treat[MASK]as an absorbing state: once a token is masked, it stays masked until the reverse process “recovers” it. This makes the corruption process native to how we handle language.
V. The Rise: Simple and Effective Masked Diffusion Language Models
This is where DLM theory starts to meet industry-grade performance. The MDLM project page also notes that the approach is used in: ByteDance Seed Diffusion, Nvidia’s Genmol.
https://s-sahoo.com/mdlm/

Figure: Simple and Effective Masked DLM (Subham Sekhar Sahoo, Marianne Arriola et al.
What you should take away from Part 1
- Diffusion LMs are iterative denoisers, not next-token predictors.
- The defining design question is: what does “noise” mean for text?
- Continuous diffusion (e.g., Diffusion-LM): diffuse in a continuous space, then decode back to tokens (the final projection can hurt fluency).
- Discrete diffusion: diffuse directly in token space via a categorical Markov chain (no continuous→discrete projection at the end).
- A common, stable parameterization is: predict an (x_0)-like distribution from (x_t), then combine it with the forward chain/posterior to construct the reverse transition (p_\theta(x_{t-1}\mid x_t)).
- Training/inference perspective: the model conditions on the entire corrupted sequence (x_t) at once (not a left-to-right prefix).
During inference, you typically run a fixed (T) denoising steps regardless of sequence length—so you don’t need “100 steps for 100 tokens.”
But a single diffusion step is not automatically cheaper than a single AR step; the speed story depends on how small you can make (T) and how efficient each step is.
What’s next (Part 2)
Two practical notes to carry forward:
- Generation speed depends heavily on the number of steps (T) and the transition/sampling design.
- Diffusion updates many positions per step, but it still needs multiple steps, so a speed win over AR is not guaranteed.
Part 1 covered the motivation and basic formulation. Naturally, that raises:
We saw the motivation of Diffusion LM and its formulation in Part 1. This would naturally make us ask
Q. What are the remaining challenges and the key recent advances?
Q. What are some practical and strong Diffusion LM Applications?
In the next post(s), I want to connect method → practice:
- Scaling & systems: what changes vs KV-cache-heavy AR decoding?
- Speed / parallelism: where diffusion helps, where it still bottlenecks
- Biology angle: why this is attractive applications?
Key references
Enjoy Reading This Article?
Here are some more articles you might like to read next: