More on Parallelism | Terry (Taehan) Kim

In the previous post, I went through an overview of strategies related to scaling. A natural follow-up question, when thinking about parallelism, is “how” and “what” the devices are communicating with each other.

More concretely:

What part of the tensor does each device hold?
What gets communicated between devices?
How does that communication resolve shape / dimension mismatches?

Walking through a simple example helps show why this question matters.

Imagine we have a tensor split across devices, but the resulting dimensions don’t match for the operation we want to do. How do we deal with that?

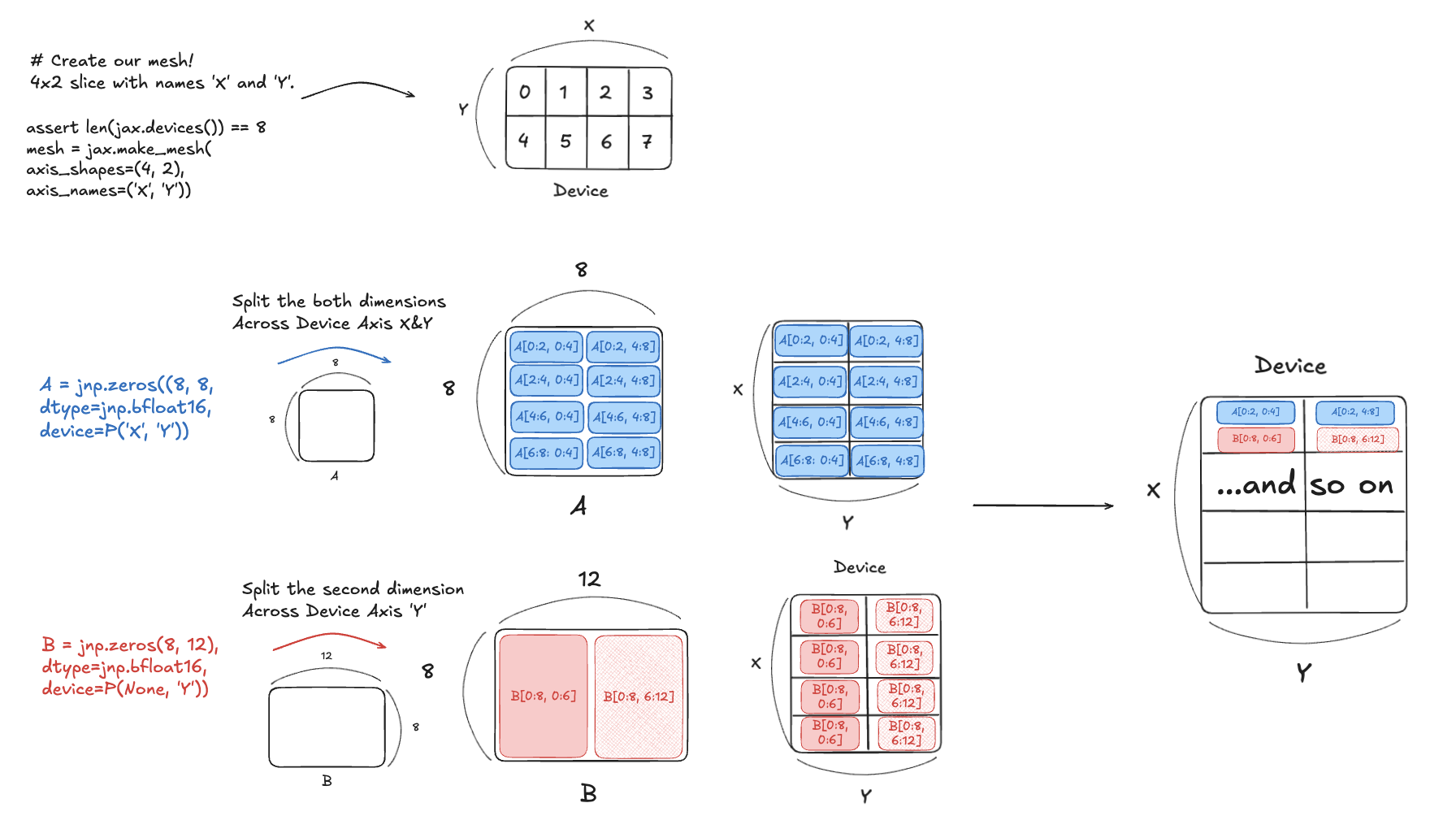
Figure: Matrix Split Across Devices

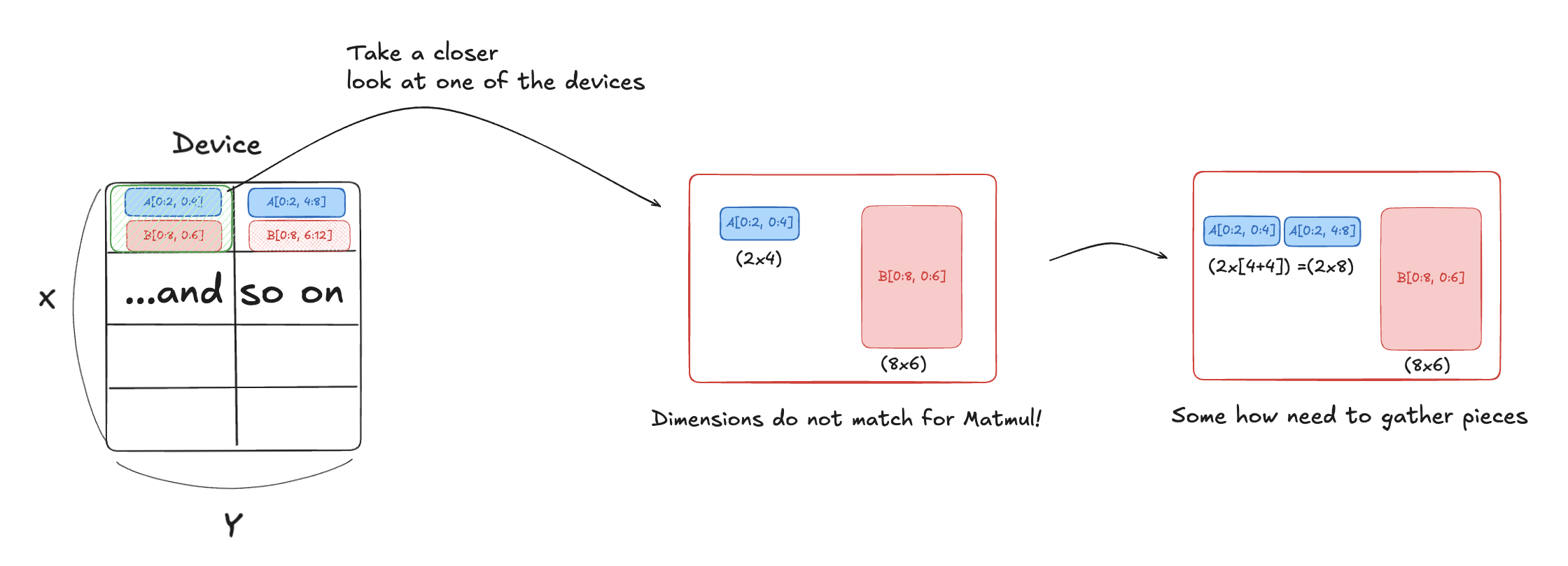
As we see from the image above, devices would have to some how communicate with each other to resolve these dimension mistmatch. This is reason why understanding this process really matters.

At a high level, two common communication patterns we can see are:

[1] AllGather

This is similar to the case illustrated in the image I drew above:

\[\mathbf{A}[I, J_X] \cdot \mathbf{B}[J, K] \rightarrow \mathbf{C}[I, K] \\ \mathbf{AllGather}_X[I, J_X] \rightarrow \mathbf{A}[I, J] \\ \mathbf{A}[I, J] \cdot \mathbf{B}[J, K] \rightarrow \mathbf{C}[I, K]\]

If one operand is sharded along the contracting dimension (here, (J)), we typically AllGather that operand first so every device has the full (J) dimension locally. Then each device can run the matmul without missing contributions.

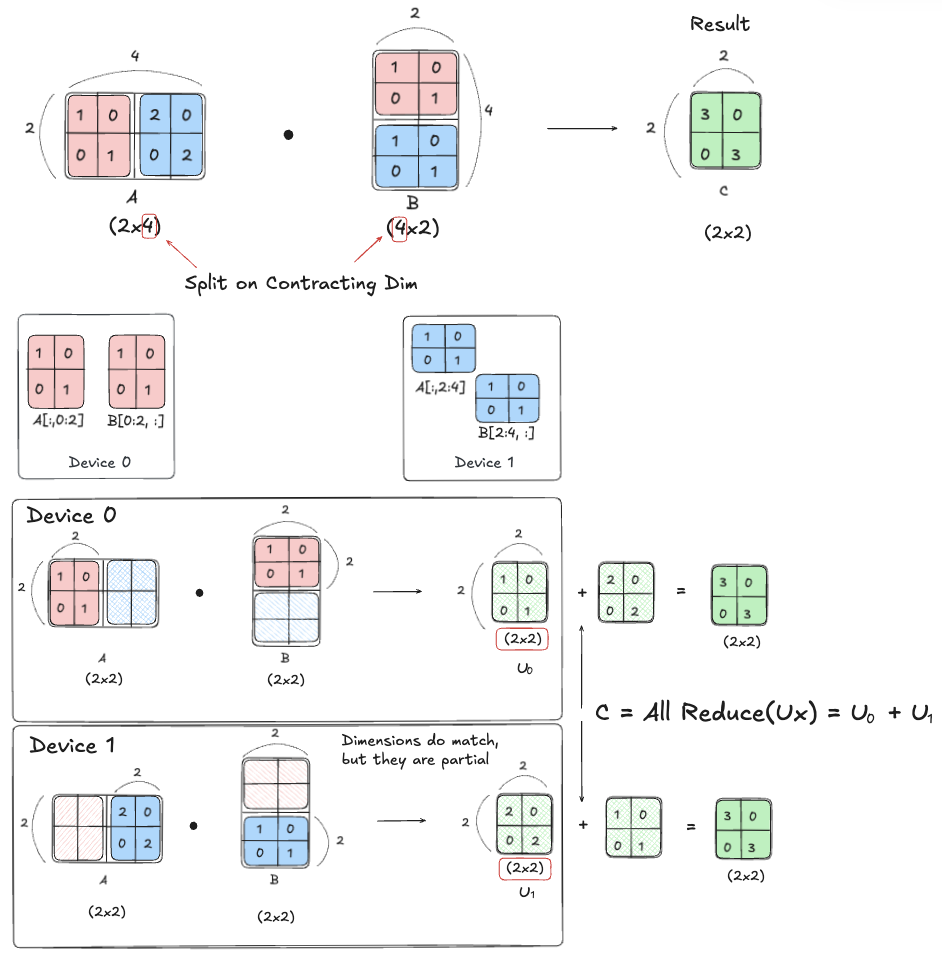
[2] AllReduce

\[\begin{align*} A[I, J_X] \cdot_{\text{LOCAL}} B[J_X, K] \;\rightarrow\; &\; C[I, K] \{U_X\} \\ \mathrm{AllReduce}_X \; C[I, K] \{U_X\} \;\rightarrow\; &\; C[I, K] \end{align*}\]

Where AllGather “gathers” pieces to form a full tensor on every device, AllReduce “reduces” (usually sums) partial results that were computed independently on each device.

This happens when the contracting dimension itself is split across devices, so each device can only compute a partial sum of the output. I have illustrated a simple example below:

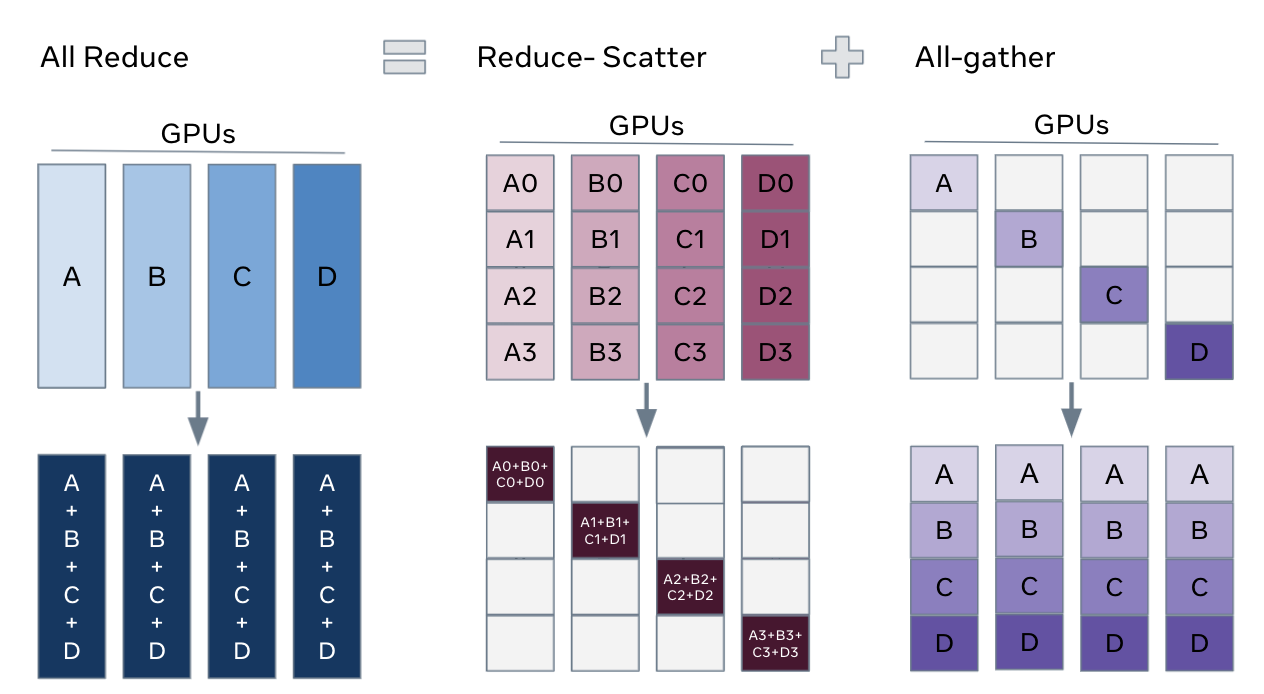
[3] AllReduce = ReduceScatter + AllGather

All Reduce can be seen as combination of two ops.

“Generally, an AllReduce is ~2× as expensive as an AllGather.”

I drew out an illustration aligned with the example we explored before:

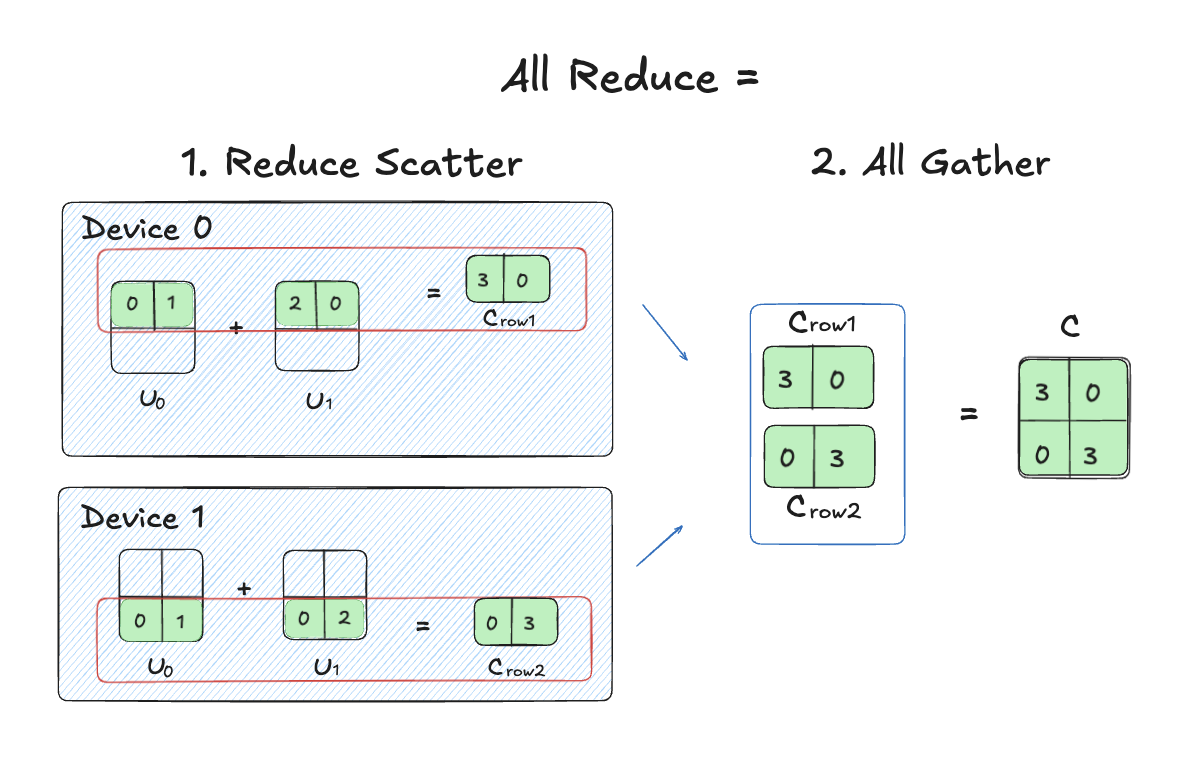
The key idea is that AllReduce (for summing partial results / gradients) can be decomposed into two phases:

ReduceScatter: sum across devices and keep only your shard
→ lower peak memory during the reduce phase
→ less data to move per step (often bandwidth-optimal)
All Gather

Auxiliary: FSDP (Fully-Sharded Data Parallelism) vs Tensor Parallel

The previous post had a more general view of parallel strategies. Now that we have a better understanding of the communication ops above, we can describe specific parallelism schemes in more detail.

FSDP (Fully-Sharded Data Parallelism)

For example, FSDP improves on pure data parallelism by significantly reducing per-device memory usage.

\[\text{In}[B_X, D] \cdot_D W_\text{in}[D_X, F] \cdot_F W_\text{out}[F, D_X] \rightarrow \text{Out}[B_X, D]\]

We can see that the batch dimension of the input data is sharded (B_X). Also notice that some weight dimensions are sharded (e.g., D_X). Since this is still “data-parallel-style” execution, each device processes its own batch shard independently. The main difference is that the weights are sharded in memory, so we need communication to make the layer’s weights available for computation.

Q. (FSDP) In the forward pass (just computation, not backprop), which operations above will we be using (AllGather, AllReduce, etc.)?

A. Typically AllGather (to materialize the full weights needed for the layer on each device, just-in-time), then a local matmul.

Tensor Parallel

\[\text{In}[B, D_Y] \cdot_D W_\text{in}[D, F_Y] \cdot_F W_\text{out}[F_Y, D] \rightarrow \text{Out}[B, D_Y]\]

It looks very similar to FSDP, but note that the batch dimension is preserved ((B) is not sharded here). Instead, Tensor Parallelism shards the model dimensions (e.g., (D) or (F)) across devices, so each device computes only a slice of the layer.

It sounds confusing, but the general rule is:

FSDP: focuses on memory distribution. FSDP shards parameters for memory savings, not to split the math.
→ (W) is sharded in memory, but each device still computes the full layer output for its batch shard, so it often needs to AllGather (W) temporarily.
TP: shards the computation itself.
→ each GPU computes only part of the matmul, and then uses collectives to combine partial results.

Key references